生日悖論（Birthday Paradox）

某一天，在一班約莫有30名學生的課堂上，老師突然提到：「我們來玩個小賭局。只要課堂的現場上，有任何兩位同學的生日是同一天的，就算老師贏；如果沒有任何人的生日是相同的，就算老師輸。如果老師輸了，就請全班喝飲料，如果老師贏，下次上課時，全班不准有人遲到。」假如您剛好是這一個班上的同學，您賭不賭？

直覺上，這個賭局似乎對全班同學很有利，看來飲料是喝定了。畢竟課堂上只有30位同學，但對應到生日，一年卻有365天，兩個人同一天生日應該很低。因為遇到同一天生日的機率為1/365，或0.002739。這機率也太小了吧，這也是在生活中，一旦您遇上到一個和您同一天生日的人，往往會讓您感慨，這也太巧了。

然而，事實上，這場違反直覺的賭局，老師贏的機率可是高達七成，這就是俗稱的「生日悖論（Birthday Paradox）」。

生日悖論是奧地利數學家理察·馮·麥澤斯（Richard von Mises），於1939年針對「資料儲存技術」所發表的論文。大致的內容以數學方式來說：若有一個均勻的映射函數將23個不同、屬於整數集的數，映射到〔1，365〕時，兩個數映射到同一位置的機率為0.5073（＞0.5）。因此，可知利用散列儲存技術查尋儲存器時，難免會發生碰撞。

翻譯成白話文的意思為「如果一間屋子裡，有23個人以上，其中2人同一天生日的機率，會大於1/2」。

要算出背後的機率觀念上不難。以30位同學為例，先計算30位同學生日都不相同的機率，第一位同學的生日有365種可能；第二位同學的生日有364種可能（因為生日要不同），第三位同學的生日有363種可能，以此類推，第30位同學生日有336種可能。

所以，30位同學生日都不同的機率為，365 乘 364乘363乘…乘336 除上 365 的 30 次方，大約是30%。所以班上至少有兩位同學生日相同的機率為1–30%等於70%。

從公式來看，所有人的生日都不相同的機率為：

P= 365*364*…*（365-N+1）365N

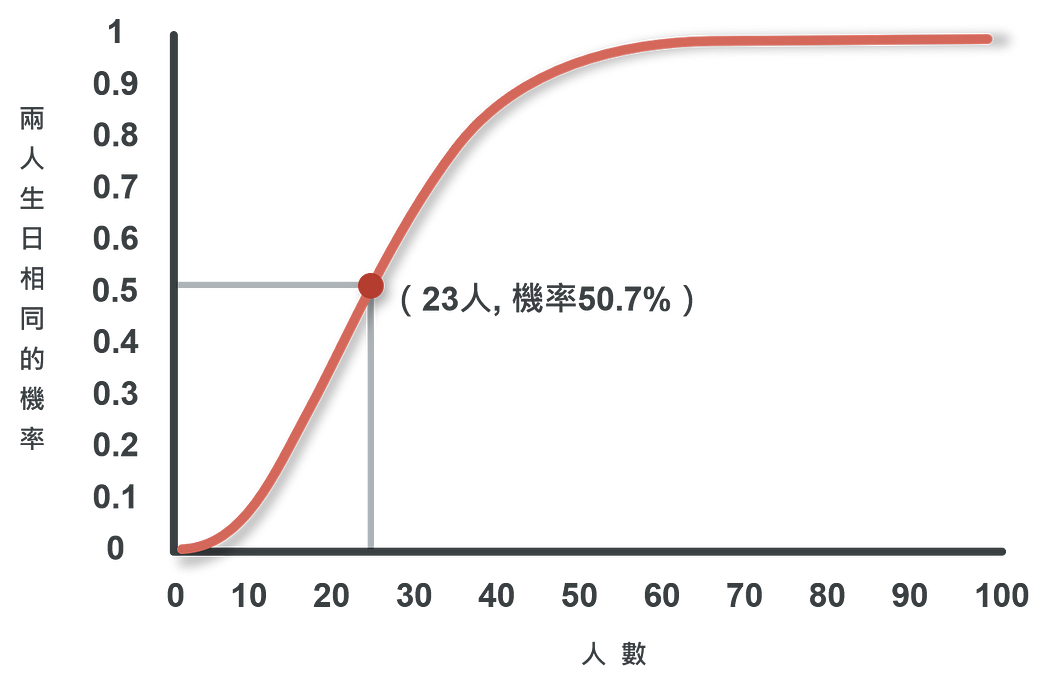
根據這項公式，n等於23人時，兩人同一天生日的機率1-P（補集），已經為50.7%，意思是，教室內只要有超過23名同學，老師贏的機率已經超過一半；當n一旦來到30人時，1-P為70.6%；而n等於50人時，1-P為97.0%；當n等於60人時，1-P為99.4%。

其實，生日悖論往往在提醒我們，「直覺」通常是不可靠的，而且統計學很重要。因此在做決策時，要儘可能地蒐集資料，並對資料進行分析，以利理性決策的進行。還有，就是千萬不要跟老師對賭，因為輸的機率很高。下次上課您就得乖乖地提早來！

作者：蘇宇暉（台科大管研所博士候選人）、羅凱揚（台科大企管系博士）

繪圖者：彭煖蘋