何謂合取謬誤（Conjunction Fallacy）？

想像一下，您正參與一項 心理學實驗。研究人員先給您看一位叫做「琳達」的背景資料。

琳達（Linda）今年31歲，單身、性格直率且非常聰明。她大學主修哲學，在學生時期，她非常關注 歧視和社會正義 的問題，當時還參加了反核示威遊行。

接著，請您就下列敘述，給予1~8分的評分，1分是最有可能，8分是最不可能，來評判琳達可能是什麼樣身分的人。

「琳達在小學教書（ 分）
琳達在書店工作並定期上瑜珈課（ 分）
琳達活躍於女權運動（ 分）
琳達是精神病院裡的社工（ 分）
琳達是某個婦權聯盟的一員（ 分）
琳達是一位銀行出納員（ 分）
琳達是一位保險業務員（ 分）
琳達是一位銀行出納員並活躍於女權運動（ 分）」

您的答案出來了嗎？

這個實驗，是由美國行為科學家 阿莫斯．特維爾斯基（Amos Tversky）和諾貝爾經濟學獎得主 丹尼爾．卡尼曼（Daniel Kahneman）所進行，該實驗被稱為「琳達問題（Linda Problem）」實驗（而之所以取名「琳達」，是因為特維爾斯基教授以他在史丹佛大學的秘書琳達．科文頓（Linda Covington）為名）。

該實驗的研究人員，向88位受試對象描述以上個案，以下是部分分數從低（最有可能）到高（最不可能）的排序。

「琳達活躍於女權運動（平均2.1分）
琳達是一位銀行出納員並活躍於女權運動（平均4.1分）
琳達是一位銀行出納員（平均6.2分）」

不知道，大家有沒有看出來這項調查結果背後潛藏的問題。問題在於第二和第三項的敘述。受試者們認為「琳達是一位銀行出納員並活躍於女權運動」高於「琳達是一位銀行出納員」。

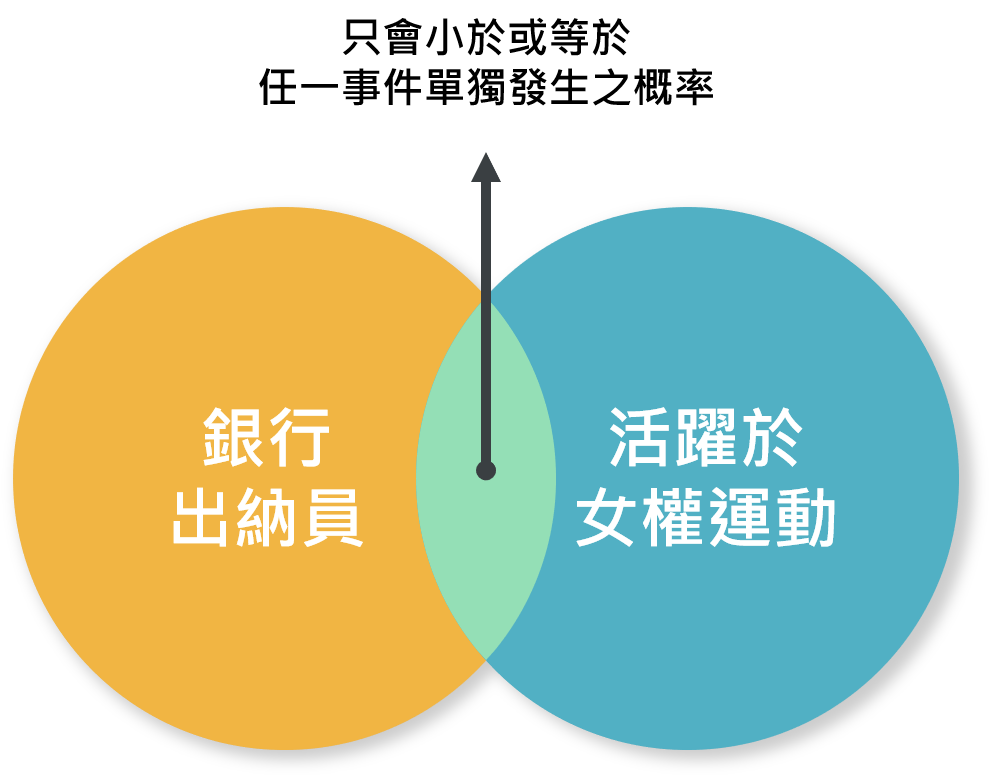
然而，特維爾斯基教授指出，從邏輯上來說，這樣的判斷其實並不合理，因為兩個事件同時發生的機率，往往都只會小於或等於任一事件單獨發生的機率。這就是所謂的「合取謬誤（Conjunction Fallacy）」。

合取謬誤又稱做「交集謬誤」，主要是人們 #習慣將多重條件「A 且（and） B」，誤認為它要比單一條件「A」或（or）「B」，更可能會發生的一種錯誤認知，如圖1所示。

最後，我們可能會認為，一位數學博士也應該很會寫程式。但數學博士與程式很強本來就是兩件事情，同時數學與程式都強的人，本來就比單獨數學強或單獨程式強的人還來的少。所以，我們要避免不自覺地掉到這樣的謬誤裡。

作者：羅凱揚（台科大企管系博士）、蘇宇暉（台科大管研所博士候選人）
繪圖者：彭煖蘋