一筆畫與柯尼斯堡七橋問題（Seven Bridges of Königsberg）

您小時候有沒有玩過益智遊戲中的「一筆畫」呢？就是一個圖型內有數個節點，然後有數條線將它串連起來。遊戲的方法很簡單，就是可以從任何一個點開始走起，必須把每個點都走過一遍，而每個點都不能重複走過，這就是一筆畫的玩法。事實上，這個俗稱一筆畫的遊戲，其實就是來自拓撲學中的「七橋問題」。

在拓撲學的歷史上，第一個的難題源自於東普魯士，普列戈利亞河畔的柯尼斯堡（今日俄羅斯的加里寧格勒）。當時的市區跨越普列戈利亞河兩岸，河的中心有兩座小島，小島與兩岸之間有七座橋相連。

由於當地的居民在散步時，常常會經過許多橋，因此便引發了一些人的好奇心，他們想了解是否有可能在每座橋只走一次的前提下，將所有橋都走遍，這就是著名的柯尼斯堡「七橋問題」。

這個問題，後來被瑞士數學家李昂哈德·尤拉（Leonhard Euler，1707~1783）（圖1 ）於1735年所解決。

尤拉發現，島與橋的實際位置及距離，並不是解決問題的重點。重要的是這些橋的連結方式。因此，七橋問題可以從實體的地圖，畫成如圖2的網路圖（上下兩個點是兩岸，中間左右兩個點是兩座島，七條線是七座橋）。還記得之前提到的捷運路網圖，以及橡皮筋幾何學，這樣看起來，這正好是個拓撲學問題。

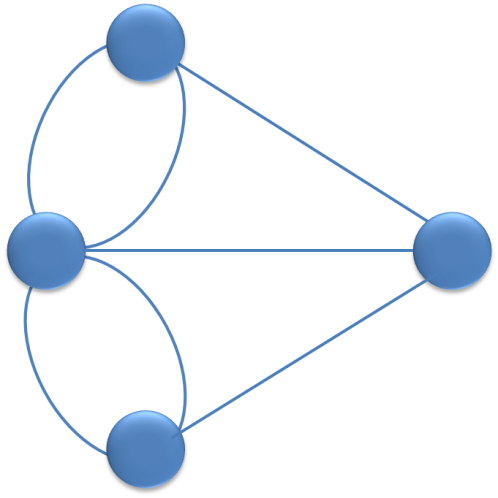
尤拉指出，網路圖中的節點，如果有奇數條線向外延伸出去，可以稱為「奇數點」；如果有偶數條線，就稱為「偶數點」。而如果這個圖形必須符合兩個條件，這個問題才有解。

首先，圖形的每個點都必須是偶數點；其次，如果圖形中有奇數點，奇數點最多也只能有兩個，因為，為了要一次走完，一定要在奇數點開始或結束，所以最多只能有兩個奇數點。至於奇數點的線條數則不一定要一樣，一個三的奇數點，可以搭配五的奇數點。

由於柯尼斯堡七橋問題的網路中，有四個奇數點，所以這個問題「無解」。如果您有興趣，不妨拿出來筆來自己畫一畫，甚至可以出題目自己來試試。

後來，尤拉更提出了「尤拉公式」來證明在平面上任何的網路，下面公式成立：

V-E+F=1

其中，
V是頂點(七橋問題中有4個點，V=4)
E是連線(或稱邊，七橋問題中有7個邊，E=7)
F是面(七橋問題中有4個面，F=4 )

有趣的是，以上所說「網路圖」的呈現與計算方式，又另外開啟了數學裡「圖論（Graph theory）」的先河，尤拉也成了圖論的開山始祖。顧名思義，圖是圖論的主要研究對象。而圖是由許多個給定的頂點及連接兩頂點的邊所構成的圖形，圖形常用來描述某些事物之間的特定關係；頂點則用於代表事物；連接兩頂點的線或邊，則用於表示兩個事物間具有的關係，而圖論往後又構成網路爬蟲（搜尋）的基礎，我們會再找機會與大家說明。

作者 : 蘇宇暉（台科大管研所博士候選人）、羅凱揚（台科大企管系博士）