Chapter 05 演算法

一、事有先緊急先後，優先佇列的處理

如果您曾到過世界各地的迪士尼樂園遊玩，您可能會發現每一項熱門的遊樂設施往往都大排長龍。像是最受歡迎、全程二分四十五秒的「太空山（Space Mountain）」，每一次玩下來卻總是要排隊一個小時。有時候，的確也因為人潮眾多，導致顧客滿意度降低。後來迪士尼樂園便推出「快速通關服務（FastPass）」，讓不同等級的遊客可以透過快速通關服務，減少遊樂設施的排隊時間。

「快速通關服務」的概念，後來被許多遊樂園區、風景區所模仿。像是免費、付費、單項、多項……等，不同形式的快速通關服務也不斷地出現。這些快速通關服務，為主題樂園帶來了更高的顧客滿意度，也帶來了更多的收益。

話說回來，快速通關服務本質上就是允許優先權高的人可以「插隊」。至於誰的優先權比較高，可以取決於誰的付費比較高（例如，在主題樂園中購買全額票的貴賓，而非購買打折又打折的離峰時段票的顧客），或是誰比較緊急（例如，在急診室裡，病人的看診就不是依照先到先看的順序，而是依據患者的重症程度）。

事實上，快速通關服務的設計，從資料結構的觀點來看，其實就是所謂的「優先佇列（Priority Queue）」概念。在此，我們先簡單介紹一下何謂佇列（Queue），再進一步說明，何謂優先佇列（Priority Queue）。

依據國家教育研究院圖書館學與資訊科學大辭典的解釋[1]，「佇列是一有序串列，若所有的插入作業在該串列的一邊進行，而所有的刪除作業在該串列的另外一邊進行，則此有序串列稱為佇列。」如圖 1 所示。

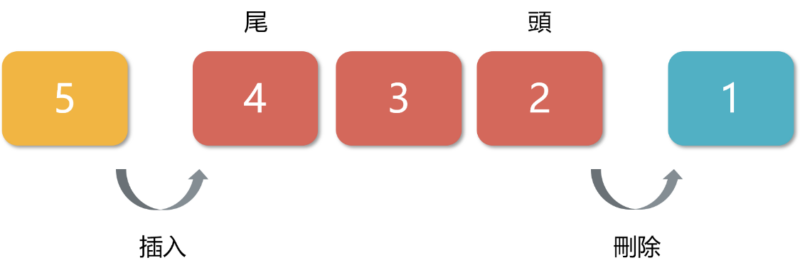
圖1 佇列

繪圖者：謝瑜倩

由於在佇列裡，最先加入的，會最先被刪除，所以佇列又有「先進先出（First In First Out，簡稱FIFO）」的特性。至於「優先佇列」，則是打破FIFO（先進先出）的規則，讓擁有優先權的人可以插隊。

在日常生活中的應用，做事比較有效率的人，常會列出「「待辦事項」。這些待辦事項表面上看起來可能沒有邏輯順序，然而實際上在執行時，還是要有「優先順序」。

舉例來說，先把待辦事項臚列出來，接著將待辦事項賦予「權重／優先權」，（亦即待辦事項的重要程度），並列舉出「最重要、……、最不重要」等項目。通常，待辦事項可能是依「先進先出（First-In-First-Out）」的順序來處理，但也有可能是依照額外賦予事項的「優先權」順序來進行。

例如，王小明每天早上起床後，固定要喝咖啡（重要性3分）；洗澡（重要性10分）；讀英文（重要性6分）。因此，依權重來進行判斷，一定就得先洗澡，再依序讀英文和喝咖啡。如果某天王小明睡過頭、時間不夠，則捨棄咖啡不喝，到辦公室後再想辦法。而某一天早上，突然門鈴響了，有快遞上門，小明勢必得拋下手邊工作，先去應門。因為如果錯過了快遞，晚一點想要再拿到包裹，可能得花更多功夫（此時，收快遞就成了第一優先）。

二、如何找到真命天子/女 - 最佳停止演算法來幫忙

「人為什麼要戀愛？因為生而為人，我們都不完整」，這是漫畫「第 N 次戀愛」的開場白。當然，從現代人的觀點來看，結婚並不一定是戀愛的最佳結局，但是您有沒有想過，如果您一生當中，打算談 N 次戀愛，您應該在談到第幾段感情後，就應該試著與對方定下來？選擇另外一半，其實也可以用數學的最佳停止（Optimal stopping）演算法，來協助做好決策。

其實，怎樣找到真命天子或天女的故事，要從企業如何「找秘書問題」（Secretary Problem）談起。假設您公司要應徵新秘書，總共有 300 人投來履歷，最後決定要面試 100 人。而面試完後，當下就得決定是否錄取，如果當下不錄取，之後也無法反悔。那麼，到底要面試幾個人，或是該採取什麼做法，才有較大的機會，找出最佳人選。

首先，請思考一下，我們的目標是找到「最佳人選」。如果只有一位應徵者時，這時錄取他就對了；如果有兩位應徵者，此時錄取到最佳人選的機率就是 1/2；如果有三位人選，直覺上，錄取到最佳人選的機率是 1/3，但透過另外一種方式，我們可以將成功機率，一樣提升到 1/2。這個方法是如何進行的？

作法如下，當我們遇到第一位應徵者時，先予以保留、不要錄取，等到第二位應徵者出現時，如果他比第一位優秀，就錄取他；如果沒有比第一位優秀，就不錄取他，繼續面試第三位，而且不管第三位面試者是否為最佳，都錄取他。然而，這種方式為什麼可以提升錄取到最佳人選的機率？

我們思考一下，從第一到第三位應徵者的優劣排列組合共有 6 種（如圖 2 所示）：

圖2 應徵者的優劣排列組合

當我們採用上述策略時（意即總共有三位應徵者，面試一位後，選擇比之前優秀的，而圖1中的紅色圈圈即為選擇的人），錄取到最佳人選（即「優」）的情境為：中、優、劣；中、劣、優；劣、優、中。六種情境中會出現三次，所以成功機率拉高到 1/2。

透過以上的選擇邏輯，一旦應徵人數擴大到 10 位時，我們應該面試 3 位，經過計算，此時的成功機率會是 39.87 %（而非 1/10）；當應徵人數擴大到 100 位時，我們應該面試 37 位，這時的成功機率會是 37.1%（而非 1/100）。

在這種情況下，找秘書問題的答案是 37 人，這就是所謂的 37% 法則。

現在話說回來，因為戀愛常把人搞的心力交瘁，或是讓人愛的撕心裂肺，如果不想在愛情關上，面試這麼多位應徵者，或是根本不想談那麼多場戀愛，就想找到生命中的真愛，有沒有更好的辦法呢？答案是肯定的。

德國馬克斯‧普朗克心理學研究所適應性行為與認知中心的教授彼得‧陶德（Peter M.Todd）教授， 1997 年發表了一篇文章「下個戀人會更好（Searching for the next best mate）」。透露了一個小秘訣，那就是將標準稍微放寬一點。

在該篇文章中，陶德教授透過模擬，證明當我們稍微放寬對伴侶的選擇標準時，如從最佳 1% 放寬到最佳 10% （請注意：1% 和 10% 兩種不同虛線），交往的對象數可從 37 人（— — 曲線的最高點），下降到 12 人（……曲線的最高點），且成功率上升到 77% 以上；如果再將標準放寬到前 25%，交往的對象數則只需要 8 人，且成功率高達 90%。如圖 3 所示。