行銷經理的經驗也可以科學化 - 用「K-means」演算法進行市場區隔 （附Python程式碼）

對機器學習演算法有所研究的人一定都聽過「聚類 （Clustering）」演算法。「聚類」，簡單地說，就是對於一組不知道如何分類的數據，利用演算法自動將相似的數據，劃分到同一個分類中。「聚類」從字面上的涵義很容易理解，可是，到底聚類演算法在行銷資料科學上扮演著什麼樣的角色呢？我們先從比較實務的角度來探討：

行銷人員要發展行銷企劃，根據STP流程 （或稱行銷策略）的第一步就是市場區隔 （Segmentation），首先決定區隔變數，然後衡量被區隔後市場的足量性、可接近性等…，假設我們「只」取得如下資料 （如圖1），可以很容易的根據特定的變數做切割：

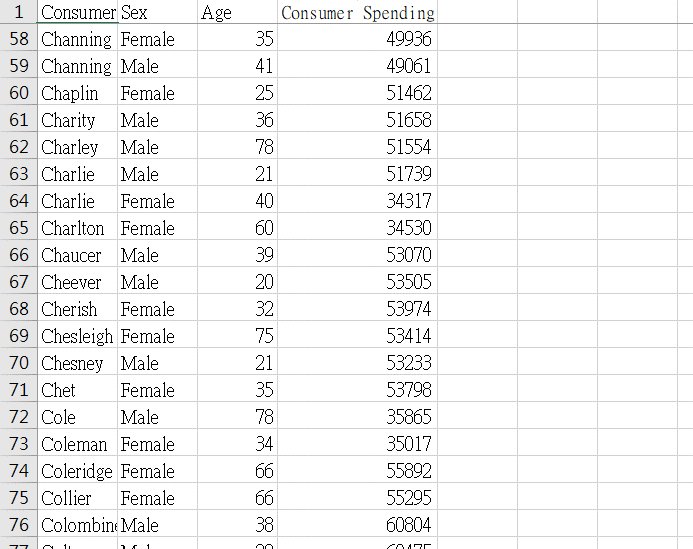
可是事情往往不會這麼順利，如果考慮的變數或資料的數量太小，分析結果很容易與真實市場情形有極大的偏差，舉例來說，當你用年齡區隔消費者的時候，寫下「我們目標族群是十八歲到三十歲的區間」然後呢？這個年齡層的消費習慣、偏好、環境、收入……等綜合條件篩選下來，是否仍值得列為目標客群?

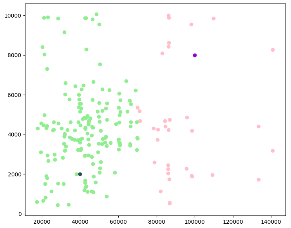
另外，就算蒐集到充足的資料，每增加一個欄位，做交互比對的時間成本也會倍增，如果資料長得像下面這樣 （圖2），即使是有經驗的行銷經理，也需要花很大的時間來了解市場全貌。

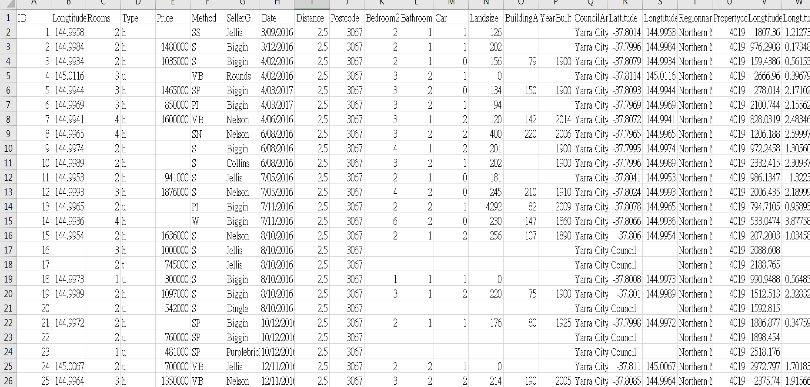
還有一個問題，人終究是人，即使經驗老道的行銷人員也不例外，要從龐大的數據中做市場區隔，很容易有認知上的偏誤。畢竟人類的理解範圍有限，很難單靠一兩個人就做完整個大規模的市場區隔，而當投入的人數眾多時，可能因為溝通、想法整合困難，反而增加成本，還不如針對少數資料做區隔來得有效。

聚類的特性在於，它不需要人員事先對消費者做分群 （非監督式學習），而是根據資料間的關聯性，將有相似特徵者自動劃分為一群，而且因為算法簡單，可以很快的處理大量資料。

換句話說，它可以一次把地理變數、人口變數等，所有能取得且有意義的欄位考慮進去，行銷人員要做的只是從這些區隔後的市場中尋找合適的目標市場，因此可以把大量需要計算與比對資料的時間留下來思考行銷策略。

為方便理解，我們假設一個情境：

我們從公司內部資料庫抓取一批涵蓋一個期間「個人消費金額」及「年齡」的數據，為了利用這些變數區隔市場，我們將資料排序後繪圖，做出了圖3 左邊的圖表!
（實際上在做分群時可能同時考慮數十種變數，簡化成兩種變數是要讓讀者容易理解）

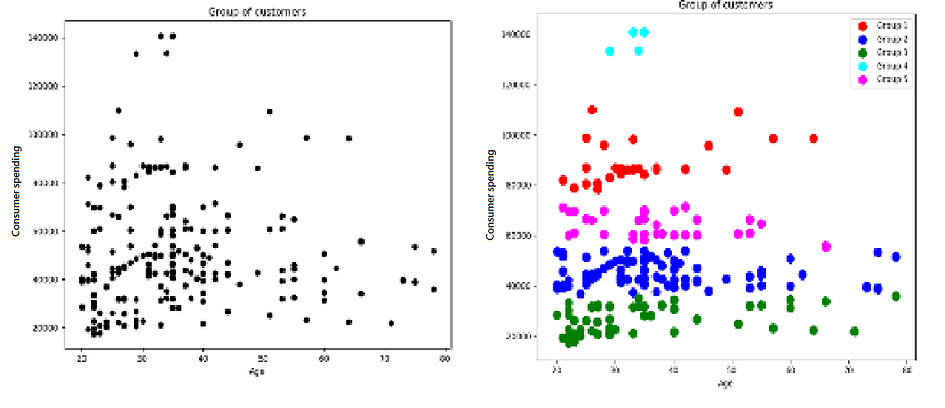
圖中的資料顯示，如果將潛在顧客依據消費金額與年齡劃分成五個群體，每個群體的顧客人數為：

也可以很容易的計算出平均消費金額：

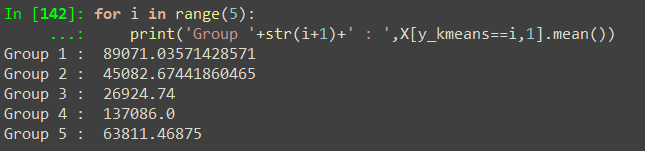
下面圖表 （圖4）的水平線就是各群體平均消費金額的位置：

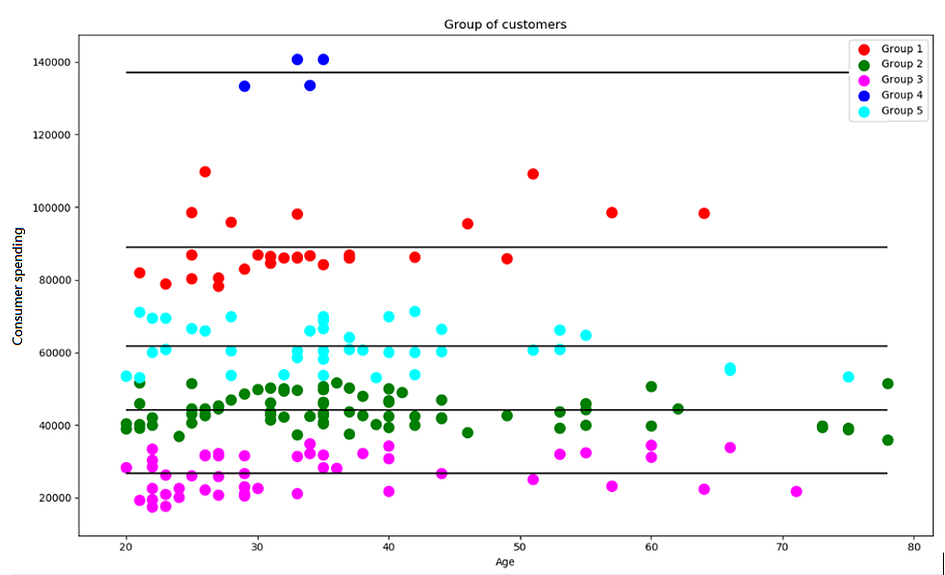
就現有資料而言，我們發現，人數最多的是下面用紅色框（圖5）起來的Group 2，平均消費金額為45,082元：

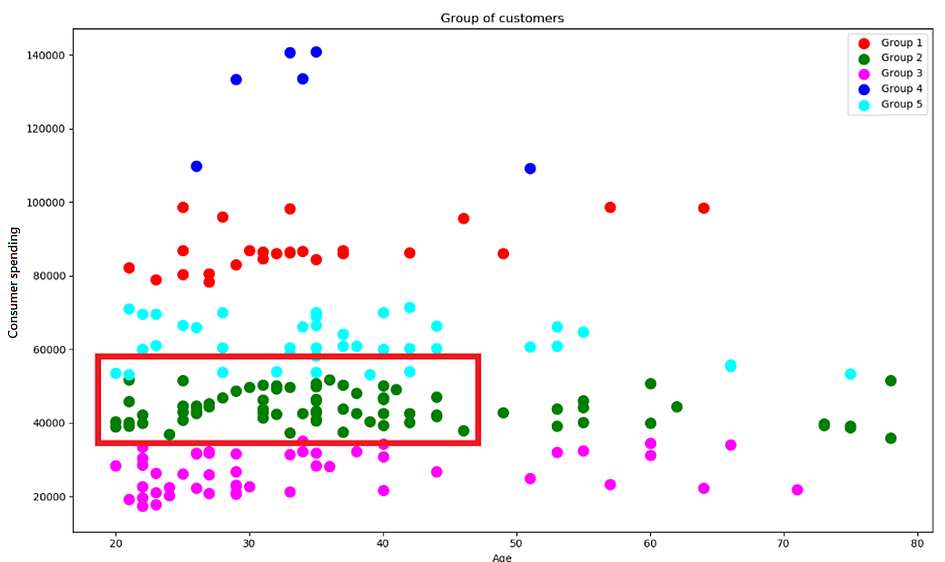
如果我們的目標客群鎖定在這個區間中，可以檢視:
1.商品定價是否符合這群人心中的合理範圍?
2.廣告性質的設計是否以這群人的偏好為主?
3.購買管道是否符合這些人消費習慣，甚至可以找這個範圍的人作深度訪談……等?
另一方面，圖中可以看出這些人的年齡分布層較為廣泛不過大多聚在20–40歲的區間，可以思考看看這些人的工作性質，日常活動時間等，如果用更多資料做交互分析，可以做更深入的分析，達到精準的市場區隔。

很難想像，過去一群行銷人員要花費數周才能在缺乏科學依據的情況下做出的市場區隔，在資料科學的時代僅需要一位資料科學家，一位具有該領域專業知識的專家就可以迅速做到，因此大量的人力成本可以省下來投入其他工作。

到底聚類是什麼東西?

接下來會用二維圖表及數學式說明K-Means演算法的流程，已經懂得讀者可以跳過這裡

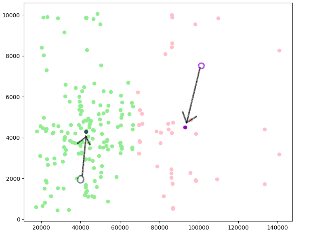
第一步:從已取得資料中任意選K個點做為聚類中心，本例中取兩點，如圖6左下角的綠點，和右上角的紫色點

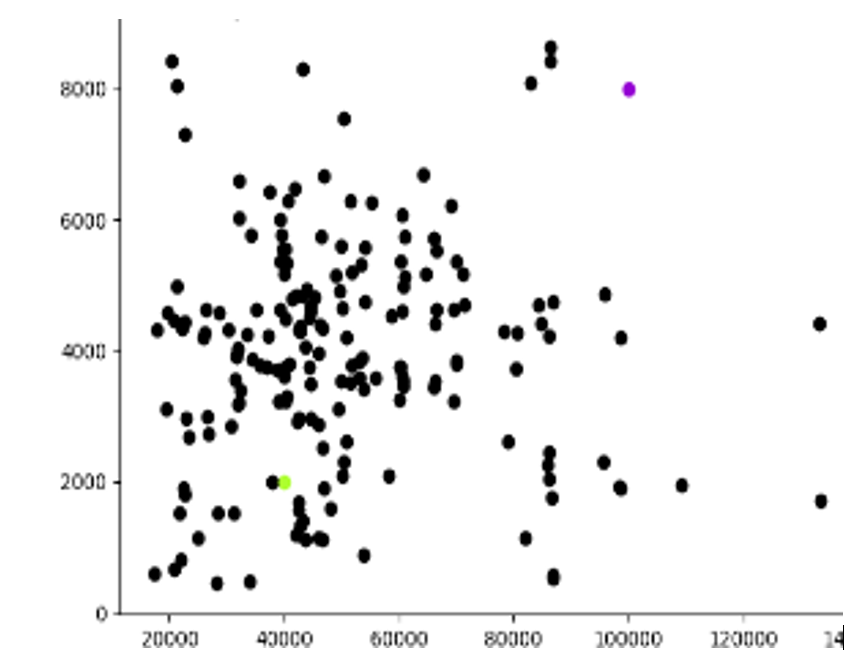
第二步:分別計算這K個中心點到所有資料點的距離(其實距離又可以分為 Minkowski Distance、CityBlock Distance、Euclidean Distance，我們這裡使用大家最熟悉的Euclidean （歐基里德）來計算距離，在一個平面座標上看起來，就是在計算三角形斜邊長度），公式如下:

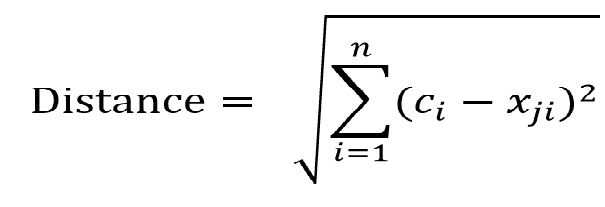
計算完後，把跟該中心距離最近的點歸為同一類，如下圖7 :

接下來，根據所有歸為同一類的的資料點座標取平均值，決定下一次的聚類中心。

下一次聚類中心的計算方式如下 :

因為有兩類資料，所以要計算兩次。

於是我們得到兩個新的聚類中心（圖8）。

根據這兩個新的聚類中心，重新將距離最近的資料點歸為同一類。

然後重複剛剛的步驟，分別計算聚類中心，然後距離，將有相同最近中心的資料歸為同一類，直到聚類中心點不再變動為止 ，如圖9（也就是說，前這一次的聚類結果與前一次相同，這樣以平均值計算的新聚類中心就不會再變動了）

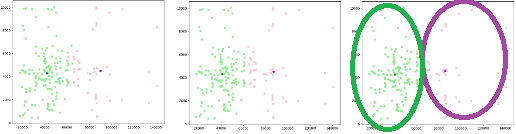
可以發現中間和右邊圖的中心點已經沒有變動了，到這裡，聚類就完成了。

最後說一下K-Means的優缺點:

優點:

1. 符合人類直覺
2. 速度快
3. 簡單易懂，不像SVM等演算法需要深厚的數學基底也可以理解
4. 可解釋性高，不像NN等神經網路的黑箱作業

缺點:

1. 結果與初始中心有關，不過這個缺點可以透過多次聚類來取得最佳結果，或是用K-mean++算法[1]來解決
2. 必須選擇所要聚類的數目。這個問題比較麻煩，因為有時我們不確定數據適合聚成多少個類別，這時可以考慮改用其他聚類方法，例如：Hierarchical clustering

善用聚類演算法，讓電腦自動做市場區隔，不但能同時做多變數分群，也可以減少人員的偏誤。

至於區隔出來的市場要如何擬定策略及方法呢? 可以利用RFM模型來討論

常貴客？新客？ 讓RFM模型簡簡單單解釋一切！ （附實現程式碼）

[1] K-Means++算法是K-Means的改良，聚類中心的初始化過程中，先隨機選取一個樣本點，然後計算這個樣本點到其他資料點的距離，選擇最遠的作為下一個初始化中心，以此類推，直到選完了第k個聚類中心點才開始執行上述演算法。

K-Means 教學程式碼：https://github.com/Charliesgithub20221030/K-Means-for-MDS-reader

作者：李政翰（臺灣行銷研究特約作者）