讓價值最大化的貪婪演算法
大家都聽過一句成語「下駟到上駟」,大意是利用次等的馬匹去和對手高一等的馬匹競賽,藉此拖垮對方,或是以下對上牽制主帥謀取勝局,而這一句其實來自「田忌賽馬」的故事,其中並牽涉到「貪心法(Greedy Method)」或是運算思維中的「貪婪演算法」。
話說齊國大將軍田忌,經常與宗族中的公子們賽馬賭錢為樂,田忌每次卻都賭輸。當時在田忌家中做客的孫臏卻發現,田忌所擁有的三匹馬的實力和齊威王的三匹馬相差不多,但卻都跑輸對方。孫臏並發現他們的馬可以分成上、中、下三等。孫臏於是偷偷告訴田忌有必勝方法,並鼓勵田忌下大賭注,保證幫他取勝。接著孫臏告訴田忌,請他先用下等馬對付齊威王的上等馬;再用上等馬對付中等馬;再用中等馬對付其他人的下等馬。最終,田忌以兩勝一敗的成績,贏了千金賭注,如圖 1 所示。
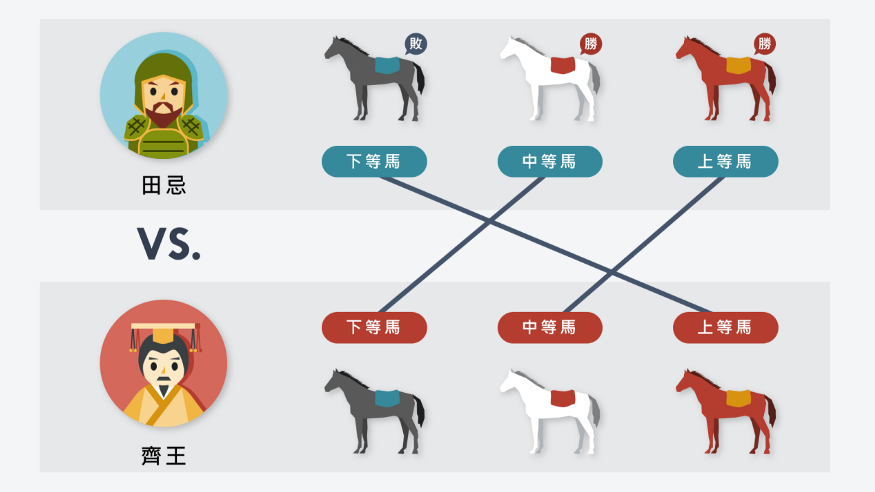
從以上的故事可發現,孫臏採取的策略其實是選擇「當下」的最佳解。當對方派出上等馬時,就用下等馬對付他;當對方派出中等馬時,就用上等馬對付他;當對方派出下等馬時,就用中等馬對付他。最終贏得賭注。而這種策略,就稱為「貪心法,或稱貪婪演算法(Greedy Method)」。
在生活中,貪心法常常都在上演,最常看到的是「背包問題」(Knapsack problem)的故事。想像一下,在您面前有一組物品,每項物品有著不同的重量與價格。現在有個背包只能負載有限的重量,此時,我們該如何選擇,才能讓背包裡的物品,總價值最高。
「背包問題」是由美國數學家托比亞斯‧丹齊格(Tobias Dantzig,1884–1956)於 1897 年所提出。而這個問題的解答,通常就採取「貪心法」來解決。
貪心法是一種採取當下最佳解,舉例來說,我們先將問題簡化成只有重量。假設航空公司的免費託運行李 30 公斤(因為難得可以搭商務艙)。這時,我們手邊有七種手提物品,重量分別為 10 公斤、9 公斤、7 公斤、6 公斤、5 公斤、2 公斤與 1 公斤。這時候透過貪心法,當下最佳解為最重的物品 10 公斤,然後在第二次的選擇中,一樣選擇剩下物品中最重的物品 9 公斤(但又不能超出限制)。依此類推,最終會選出 10 公斤、9 公斤、7 公斤、2 公斤與 1 公斤共 29 公斤的物品組合。讓手提物品僅剩下 6 公斤、5 公斤兩樣。
不過,讀者們可能會發現,這樣的結果還未必是最好的。選擇 10 公斤、9 公斤、6 公斤與 5 公斤的物品,共 30 公斤,手提物品僅餘 7 公斤、2 公斤與 1 公斤三樣,才是真正最佳的選擇(或是 10 公斤、7 公斤、6 公斤、5 公斤與 2 公斤,共 30 公斤也行)。
貪心法是一種選擇「當下」最佳解的方法,但每次最佳解的加總,有可能是「整體」的最佳解(就像田忌賽馬),但也可能未必是「整體」的最佳解(就像託運行李)。至於如何找到「整體」的最佳解,之前分享的「窮舉法」,就是一種愚笨但是有效的方法。
好了,話說回來,如果您現在正好在某個大型超市結帳,櫃檯結帳員告訴您獲得一次三分鐘的「限時搶搬貨物」機會,這三分鐘搶搬回來的商品都免費,如果利用「貪心法」,您會如何採取何種策略呢?答案當然是去把最高單價的商品找出來,搬個幾樣,就可以讓價值最大化。
作者:羅凱揚(台科大企管系博士)、蘇宇暉(台科大管研所博士候選人)
繪圖者:彭煖蘋
更多商普好文推薦
今天出門穿什麼?時尚電商Stitch Fix
時尚電商背後的行銷科學-解密Stitch Fix 「穿衣服是大學問」,不相信可以問問很多女生,每天出門前會不會為了今天要穿什麼衣服而傷腦筋?
