捷運路網圖與拓撲學(Topology)的故事
現在在台北,許多人每天都搭乘捷運上下班,往來台北市和新北市,捷運已成為大台北都會區最便捷的交通工具。偶爾您可能也會搭著捷運到某一站去和朋友見面吃飯,這時候我們往往會用上Google Map,請「谷歌大神」指點一下迷津,看看捷運經過哪些站,並預估一下多久會抵達目的地。
舉個例子來說,我們要從台北火車站到淡水時, 利用Google Map搜尋捷運路線時,大概會搜尋到如圖1的圖形。
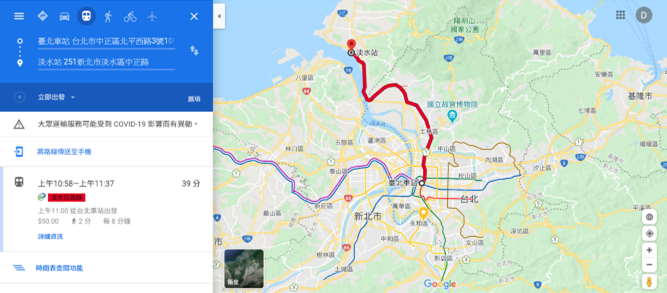
接著到了捷運上,我們也可以在台北捷運公司的網站上,看到類似圖2的捷運路網圖。但您有沒有想過,如果拿兩張圖來做比較,圖2其實不是一張合格的地圖(畢竟跟真實地圖差異太大),但我們卻也能依賴它,讓它帶我們到達目的地。
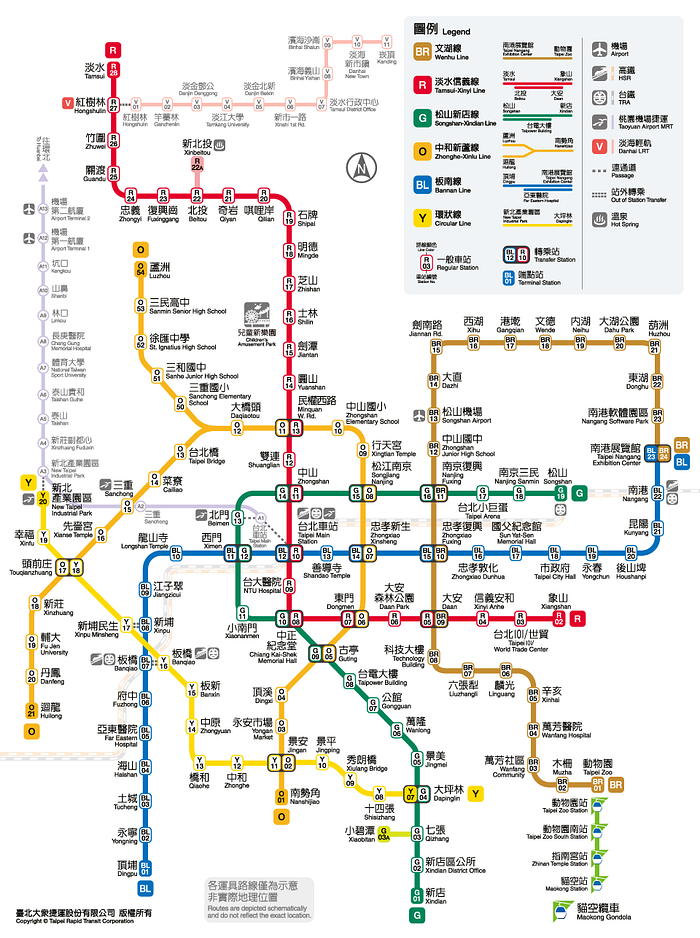
網站著作權為臺北大眾捷運股份有限公司所有
其實,對於大多數人來說,圖2比圖1簡單易讀,而圖2的價值,就在於它的「不精確」。整張圖只有交會位置與順序正確,其他部份不但距離錯誤(站與站之間的距離長度不會差不多)、方向錯誤(例如板南線往頂埔方向不是往南,而是往西南)、連路線也非直線(文湖線從劍南路到葫洲就不是一直線)。
然而,這張圖之所以有價值,即在於它只呈現出讀者想要知道的資訊:例如,應該在哪裡上車?在哪裡下車?在哪裡改換路線?讀者不需要知道的其它資訊,這張圖盡可能忽略。
好了,回到我們今天要講的主題,上述捷運路網圖的故事,其實是一個被稱為「拓撲學」的概念。
拓撲學(topology)的英文,是希臘字topos(位置)與logos(理、道)的組合,它是數學的一個分支。主要在研究空間內連續變化(如拉伸或彎曲,並不能黏合或加以撕裂)下,維持不變的性質。
在二維拓撲學裡(地圖是二維),我們可以將拓撲學想像成是一種「橡皮筋幾何學」。將橡皮筋做拉伸,只會影響路線圖的長短與方向,不會影響路線圖上每個車站的順序。所以,當拉伸路線圖上的線條時,並不會改變整體路線圖的架構。除非切斷其中的點或線,否則架構不變。而這樣的特性,經常被拿來當成科幻電影的題材。
如果各位看過「復仇者聯盟:終局之戰」這部英雄電影,劇情中,鋼鐵人東尼‧史塔克原本不願意協助未消失的英雄們,去將全宇宙消失的另一半人口找回來。後來他在家利用拓撲學中的重要物件「莫比烏斯帶(Möbiusband)」,藉此驗證出「時空旅行」的可行性。因此開始執行「時空攔劫(Time Heist)」,用量子隧道分別到不同的時間和地點,找回六顆無限寶石,讓英雄故事才得以持續下去…(好像有點扯遠了)。
值得一提的是,前述的捷運路線圖(甚至是全世界的車站路網圖),其背後的原創是來自於1931年,英國一位名為亨利‧貝克(Henry Beck)的地鐵製圖員。而這種不畫比例尺,並藉由不同顏色標示路線與站名,兩點之間的相對位置及距離,也可能與實際狀況有些差異的地圖,被稱為拓撲地圖(Topological map)。
作者 : 羅凱揚(台科大企管系博士)、蘇宇暉(台科大管研所博士候選人)
更多商普好文推薦
AI對專業服務公司行銷實務的影響 — 關係強度轉變為關係和產品的組合
AI對專業服務公司行銷實務的影響 - 關係強度轉變為關係和產品的組合 延續上一篇文章,本篇文章將進一步討論人工智慧(AI)對專業服務公司(例
