『物以類聚』分析法？K means 演算法

一家電信公司的客戶可能高達數百萬人，其中有些人就是天生愛講電話的高資費用戶，有些則只是喜歡用文字傳訊的數據用戶。如果把這些資料全部收攏在一起，做從高到低資費的排列，其實很難管理。

因為從電信公司的經營觀點來看，照顧好一個月繳交數千元電話費用的高資費客戶，遠比服務一個月只繳一百多元基本費用的客戶來的重要。理論上，電信公司應該要花更多心力，在這些高資費客戶身上，畢竟漂亮的羊毛大都出在漂亮的羊身上，照顧好這些漂亮的羊，才能獲得最大利潤，這也就是所謂的「分群管理」。

在演算法中的集群分析裡，K平均法（K-means）是一種將樣本觀察值加以分析，主要將具有某些共同特性者先整合在一起，然後分配到特定的群體，最後形成許多不同集合集群的一種分析方法。

K平均法(K-means)是由麥昆(J. B. MacQueen)於1967年正式發表，由於原理簡單、計算快速，頗受歡迎。而其就是將異質的群體區隔，分成一些同質性較高的子群組或集群，不需要事先定義好該如何分類，也不需要訓練組資料，而是靠資料自身的相似性集群在一起，最常使用在市場區隔的應用上。

我們以下面的例子加以說明，假設有9個資料點，如下表所示，此9個資料點的分布圖，如圖1所示。這樣的集群分析的目標，在於將這9個資料點，分成3群（即k=3）。

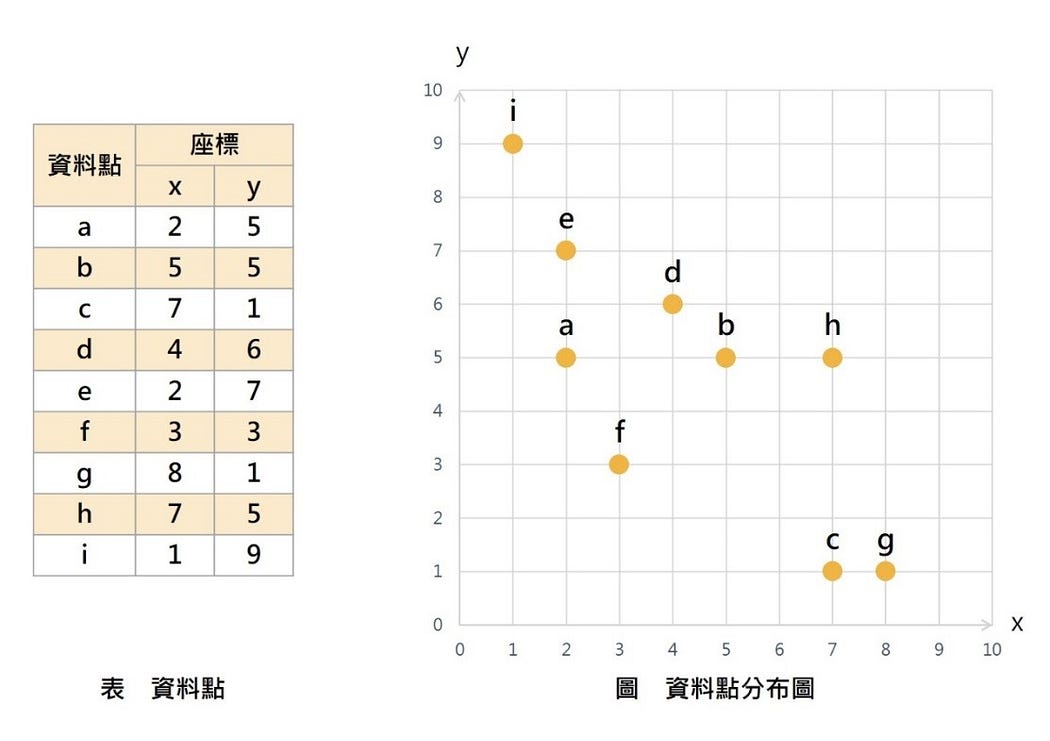
首先，隨機選出3個資料點，當成這3個集群的中心點（本例選用a、h、i三點），分別為m1、m2、m3。如圖2所示。

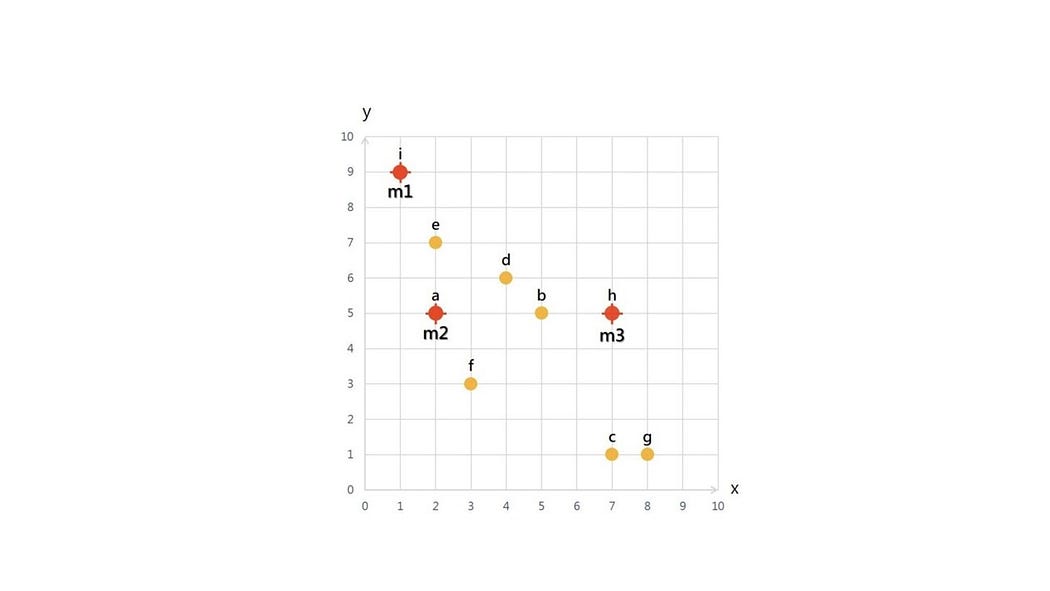
接著，由這3個資料點為起點，計算圖中每一個點與這3個資料點之間的距離，如表1所示。再將每個點，依其最短距離，將資料點歸屬於該集群（與m1的距離最短，即歸屬為集群1，與m2的距離最短，即歸屬為集群2，以此類推）。並建立出第一輪的3個集群，如圖3所示。

計算各資料點與m1、m2、m3的距離，可透過三角形公式a2 + b2 = c2來進行。以a與m1的距離為例，即為√(42+12)=4.12。以此類推。

。

之後，找出每一個集群的新中心點

New m1 = {1/1,9/1} =（1,9）

New m 2 = {（2+4+2+3）/4,（5+6+7+3）/4} =（2.75,5.25）

New m 3 = {（5+7+8+7）/4/,（5+1+1+5）/4}=（6.75,3）

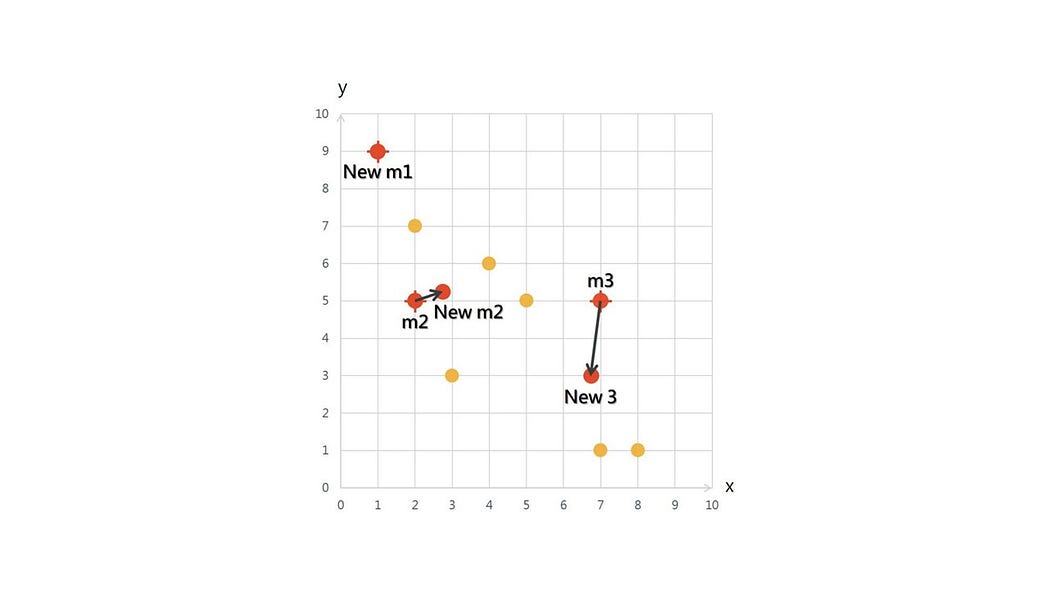
第一次集群後，產生的新中心點，如圖4.所示。

接下來進行第二次的集群，重複以上的步驟。

首先，計算各資料點與新中心點的距離，並根據最短距離進行分群。

所歸屬的集群如圖5. 所示。

接著，再找一次集群的新中心點。

NNew m1 = {1/1, 9/1} =（1,9）

NNew m2 = {（2+5+4+2+3）/5,（5+5+6+7+3）/5} =（3.2,5.2）

NNew m3 = {（7+8+7）/3,（1+1+5）/3}=（7.33,2.33）

第二次集群後的新中心點，如圖6.所示。

接著，再進行第三次的集群。

找出資料點與新中心點的距離，並根據最短距離進行分群，如表3.所示。

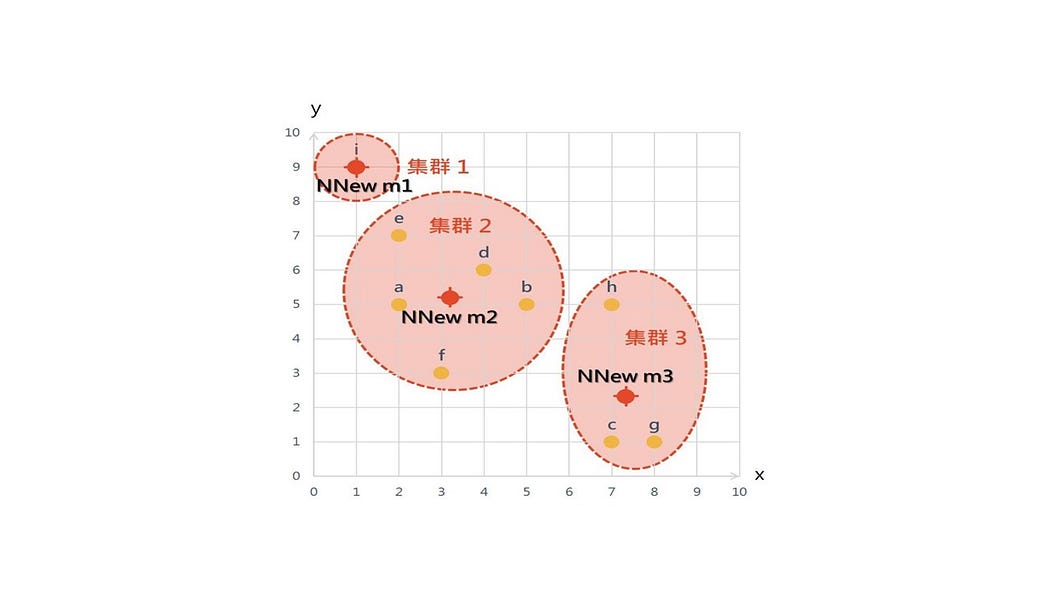
由於此次分群的結果，如圖7.，與上次相同，因此集群結束。最後，值得注意的是，K平均法（K-means）雖然簡單，但因為一開始中心點的設定，屬於隨機，所以每次跑出來的集群結果可能不同。

講了半天，各位讀者可能要問，分群之後，到底要做什麼？其實就是讓百貨公司可能清楚區分出，哪些客戶是要替他們舉辦封館特賣會的「超級VIP」；哪些是出手大方，卻已經有些時日沒有上門，必須要寄送新品發表會通知的「大咖消費者」；哪些又是還在觀望卻連會員卡都還沒有辦的「路人甲」消費者，又該用什麼見面禮吸引他們加入購物行列。對一個擁有數十萬或數百萬客戶的企業來說，不做分群行銷，其實是不夠聰明的。

作者：蘇宇暉（台科大管研所博士候選人）、羅凱揚（台科大企管系博士）