再探「合取謬誤」!

先前我們簡單介紹了「合取謬誤（Conjunction Fallacy）」的概念，讓人們了解到自己會把許多事情包裹來看，因此容易犯了邏輯上的交集謬誤。而「琳達問題」也引發了數以百計的後續研究，這裡，我們要來談談其他學者對「琳達問題」的批判。

還記得「琳達問題」嗎？
複習一下上篇何謂合取謬誤（Conjunction Fallacy）？

德國柏林普朗克人類發展研究院（Max Planck Institute for Human Development）的拉爾夫．赫特維格（Ralph Hertwig）與格爾德．吉格倫澤（Gerd Gigerenzer）教授，在1999年的《Journal of Behavioral Decision Making》發表了一篇文章〈The “conjunction fallacy” revisited : How intelligent inferences look like reasoning errors〉。裡面提到：

在琳達問題的題目中，問題是這樣問的：

Which of the following alternatives is more probable？
請問下列敘述何者比較可能為真？

Linda is a bank teller.
銀行出納員。

Linda is a bank teller and active in feminist movement.
銀行出納員並活躍於女權運動。

赫特維格與吉格倫澤教授認為，問句中的probable與and，在邏輯上具有明確的「數學意義」，但受試者在接受實驗時，看到這些字詞，所認知到的語意並非數學意義。

首先，赫特維格與吉格倫澤教授請受試者使用其他字詞，向不懂「Probable」意義的非英語母語人士，解釋琳達問題。結果，大部分的受試者都採用「非數學意義」，而不是「數學意義」。赫特維格與吉格倫澤提到，這個實驗顯示，面對語意模糊的字詞，人們往往根據對話直覺，而非抽象邏輯來推論其語意。

接著赫特維格與吉格倫澤教授將琳達問題裡，問項中語意模糊的Probable，改成意思清楚的How many，題目如下：

假設有一百人符合上述有關琳達的描述，請問這一百人，有多少人是：
銀行出納員
銀行出納員並活躍於女權運動

結果答案與「琳達問題」實驗結果完全相反，如圖1所示。

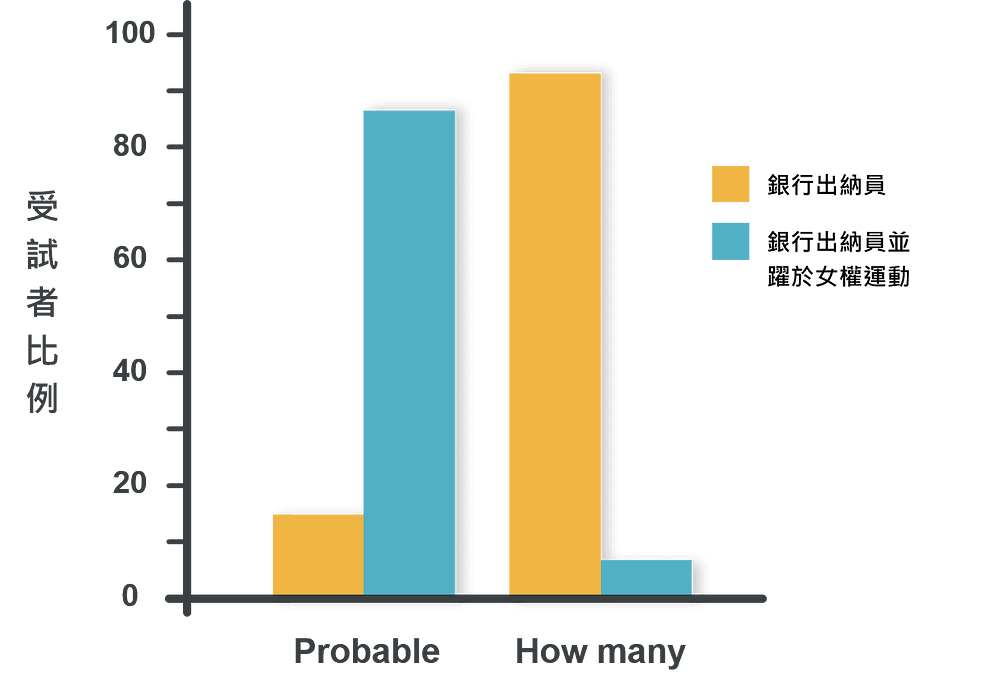
資料來源：Gerd Gigerenzer，Gut Feelings

至於「and」，在邏輯上，A and B中的A、B，具有可交換性，也就是說，「A and B」等於「B and A」，但在自然語言處理上不能這樣相互「等於」。

吉格倫澤教授舉例，請看以下兩句話：

A句Mark got angry and Mary Left.（馬克生氣了，所以瑪莉離開了。）

B句Mary Left and Mark got angry.（瑪莉離開了，所以馬克生氣了。）

如果將A句中「Mark got angry（馬克生氣了）」和「Mary Left（瑪莉離開了）」在and的前後位置交換，句意就很不一樣。

A句中Mark got angry and Mary Left（馬克生氣了，所以瑪莉離開了），很可能是因為馬克在某個場合大發雷霆，導致瑪莉決定離開。

B句中，Mary Left and Mark got angry（瑪莉離開了，所以馬克生氣了），很可能是瑪莉不告而別，讓馬克暴跳如雷。這兩句話的意思，明顯意義不同。

赫特維格與吉格倫澤教授認為，對於「邏輯」的癡迷，往往會讓人提出錯誤的邏輯問題，而錯過有趣的心理學問題。

作者：羅凱揚（台科大企管系博士）、蘇宇暉（台科大管研所博士候選人）

繪圖者：彭煖蘋

資料來源：Hertwig, Ralph; Gigerenzer, Gerd （1999）. “The ‘Conjunction Fallacy’ Revisited: How Intelligent Inferences Look Like Reasoning Errors”. Journal of Behavioral Decision Making. 12 （4）: 275–305.