世界其實不完全隨機，「規則總有例外」 - 
班佛定律（Benford's Law）

喜歡到公眾圖書館借書和看書的民眾，往往會發現，某些暢銷書或者經常被翻查的字典，前面數十頁的頁面，常被人翻爛。有趣的是，人們這種特異的習慣，竟然能演變成一項別名為「骯髒頁面效應」的班佛定律（Benford’s Law）。因為人們去找資料，理論上應是一種隨機行為，但是班佛定律卻發現，以數字1為開頭的頁面，要比以2開頭的頁面來的破舊，而以2為開頭的又比3為開頭得頁面來的舊，這個現象一直延續到9為開頭，更重要的是，現實生活中如果資料未依循這個「不隨機」，可能其中就有「詭」。

值得一提的，班佛定律其實不是班佛發明的[1]。它最早是由美國天文學家西蒙‧紐康（Simon Newcomb）於1881年，在一次不經意地翻閱「對數表」的書時，發現數字以1為開頭的頁面(不會有0的書頁)，比2為開頭的頁面來的破舊，而以2開頭的頁面又比以3為開頭的頁面來的舊。

但此時，紐康的班佛定律也還未真正成形。一直到了1938年，美國奇異公司一位電機工程師同時也是物理學家法蘭克．班佛（Frank Benford），在總部的實驗室裡，查閱對數表時也發現類似的狀況。他同時蒐集超過2萬筆各種不同的資料，一樣也都遵循類似規律。

按理，如果在一大堆的數字報表中，從1開頭到9開頭，所有的數字都應該是隨機分佈，它們出現的期望值應該都是1/9。但是班佛定律卻發現，從1到9，每個數字出現在第一位數的機率卻大大不同。以1為開頭數字的數，出現的機率大約是總數的1/3，與一般人認知的1/9差異高達3倍。同時，數字從小到大（從1到9），作為開頭數字的機率依序遞減，而越大的數，以它為首幾位的數出現機率越低，如圖1所示。

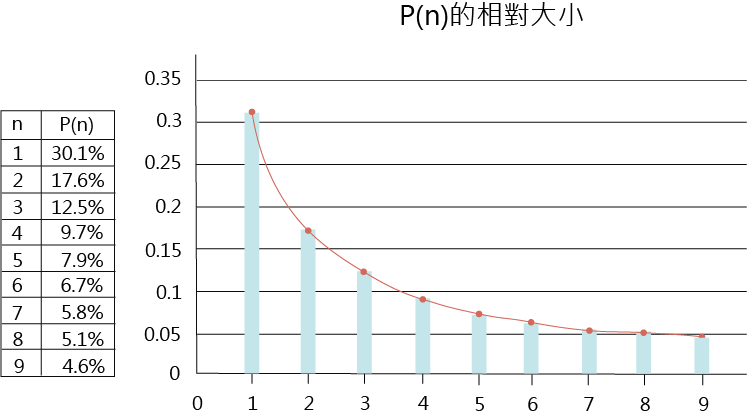
至於為何會如此，則一直等到1995年，美國喬治亞理工學院的數學家泰德‧希爾（Ted Hill）[2]才提出班佛定律的證明。他指出，紐康的想法大概是因為在社會上大多使用十進位制，因此以數n起頭出現的機率，大約會等於以10為底的log(1+1/n)。因此首位數是1的數字，出現機率即為log(1+1/1)=log2=0.3；首位數是2的數字，出現的機率為log1.5=0.176；首位數是9的數字，出現的機率是log(10/9)=0.046。

值得注意的是，班佛定律在實際運用上有不少的限制，像是資料樣本至少要3,000筆以上；其次，不能有人為限制，例如：身分證、電話號碼等，都因為有特定的人工限制在其中；其它像年紀和身高、體重也都有上下限制，而無法使用。

不過，班佛定律非常適合用來稽核各種數據是否造假，尤其是財務報表上的數字。美國國稅局曾經利用班佛定律找出是否有逃漏稅的可能。此外，班佛定律的應用還可擴大到其他領域，包括各國鄉鎮的人口數（在台灣，以1為開頭數字的鄉鎮人口數就佔了29.3%）、各國的GDP、領土大小…等。

班佛定律告訴我們，這個世界其實不完全隨機，因為「有規則總有例外」，台灣就曾有會計師運用班佛定律，抓到虛報競選經費用的真實案例，因為當事人報了太多筆的8,000元的薪酬支出，用excel報表跑資料時，就明顯發現8字頭的數字高到不像話。

[1]這又是一項史帝格勒定律（Stigler’s Law）的範例。

[2]T. Hill (1995) Base-invariance implies Benford’s law, Proceedings of the American Mathematical Society 123, 887–895.

作者：蘇宇暉（台科大管研所博士候選人）、羅凱揚（台科大企管系博士）

繪圖者：謝瑜倩