主觀機率與貝氏定理

　　先前我們曾經提過，機率可以分成「客觀機率」與「主觀機率」。客觀機率主要與頻率有關，像是當丟一枚公平銅板的次數越多，出現正面或反面的機率就會越接近0.5。這種客觀機率，強調在相同條件下的反覆執行，而且每次執行之間的結果是彼此獨立。每一次的丟擲結果，都不會影響到下一次。

　　不過，在日常生活中，許多事件背後發生的機率，卻非客觀機率。一方面，這些事件發生可能與之前事件有關（舉例來說，某一家企業這一次併購案的成功機率，就與該企業上一次併購的經驗有關）。而一旦所要進行的事件，如果本身缺乏前例可循，自然就無法計算出客觀機率。所以，在這種情況下，主觀機率應運而生。

　　十八世紀，英國有一位牧師托馬斯·貝葉斯（Thomas Bayes），提出一種作法，在估算某一個事件的機率時，可以先用主觀的方式，給予一個數值，然後檢視實際執行的狀況，再來修正最初的設定值。

　　舉例來說，您遇到了一位心儀的對象，想要判斷是否值得進一步交往。這時，您先給予「值得交往」與「不值得交往」的機率，各設為0.75與0.25。接著，透過與他（她）進一步接觸的過程，觀察他（她）是否會說謊、是否貼心、是否會遲到……等，來修正之前初始的設定。

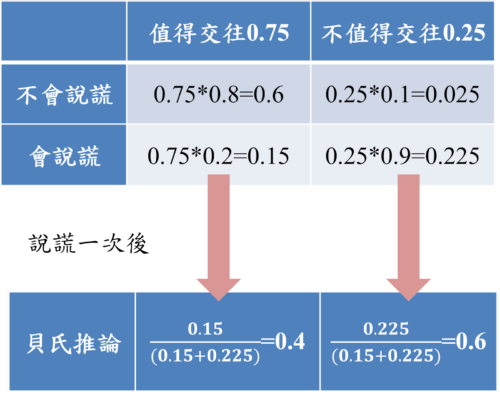
　　例如，假設「值得交往」的人，有80%不會說謊，有20%會說謊；假設「不值得交往」的人，有90%會說謊，有10%不會說謊。所以值得交往且不會說謊的機率是0.6（0.75*0.8）；值得交往且會說謊的機率是0.15（0.75*0.2）；不值得交往且不會說謊的機率是0.025（0.25*0.1）；不值得交往且會說謊的機率是0.225（0.25*0.9）。

　　接著，原本你還抱著心有好感，但是在與對方交談的過程中，你卻發現對方竟然說了一次謊。此時，在貝氏推論下，從「值得交往且會說謊」與「不值得交往且會說謊」的兩種機率中，則可進一步推論出「值得交往」與「不值得交往」的機率。

　　這時可以發現，值得交往的機率從原本的0.75，一下子降到0.4（0.15/（0.15+0.225））；不值得交往的機率，反而從0.25提升到0.6 （0.225/（0.15+0.225）），如圖1所示。